Template Models for Bayesian Networks

PGM week 2 started from December 11th, 2016. Professor Daphne, Koller mainly focused on description of template models and typical model definition.

1. Overview of template model

Motivation: to reuse commonality of different specific Bayesian Network. Taking Genetic inheritance as example, see Figure 1-1.

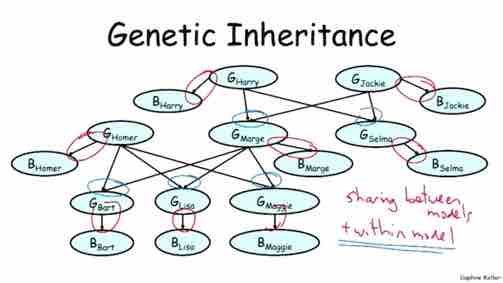
Figure 1, models with shared information Taking genetic inheritance as example, major commonalities include as follow:

1. Share between models
   Example: different family to share same "abstract" Bayesian Networks to avoid construct BN for each case
2. Share within models
   Example: Gene to Blood probability reasoning pattern from parents to child

Other PGM applications:

1. NLP Sequence Model
   Example: PGM Model to predict words' property, B-LOC, L-LOC, etc. are independent with model in named entity recognition
   

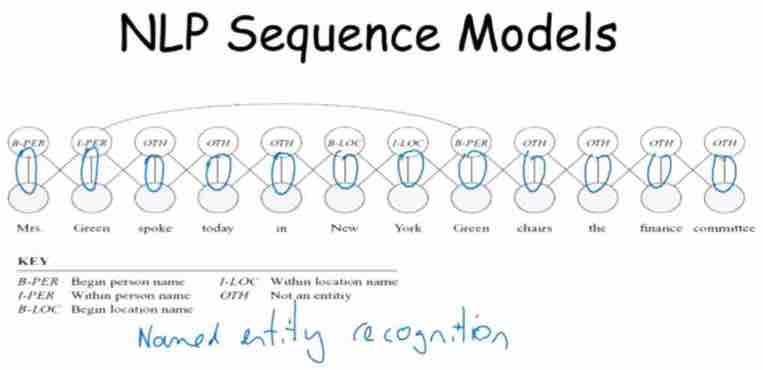
Figure 1-2, NLP model

1. Image segmentation
   Example:

• Category processing of superpixel algorithm could be abstractly shared logic
• Relationship processing of pair of superpixel Si->Sj algorithm could be shared for different image
• Shared across model between different images in abstract model

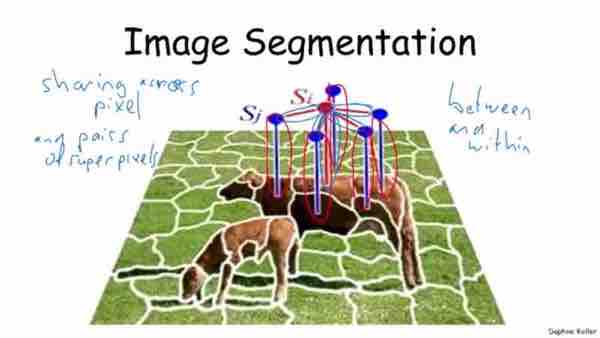
Figure 1-3, Image segmentation

1. University grade prediction
   Example:

• Shared structure for difficulty of course, intelligence of student, grade of student in course
  

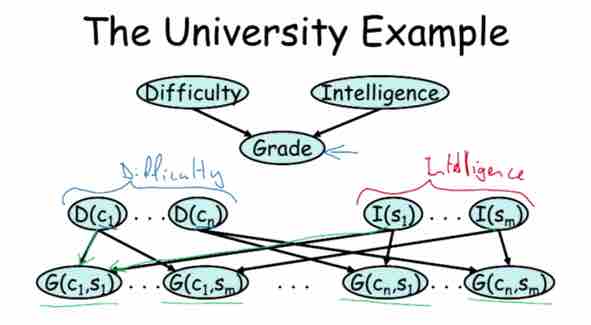
Figure 1-4, University Example 4. Robot localization prediction

Example:

• Position X(t) (position on time t) depends on previous position X(t-1) and control signal U(t-1)

Figure 1-5, Robot Localization Use Case

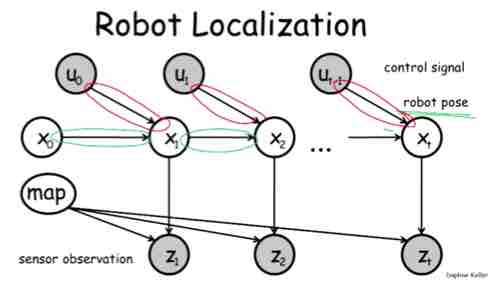
Figure 1-6, Robot Localization Model

Definition

1. Template variables: $X(U_1,...,U_k)$ is instantiated by multiple times
2. Template model: specify how variables(grand variable) inherits dependency model from template

2. Temporal model - DBNs

• Definition: temporal models evolved over time
• Distributions over trajectorises
• Pick time granularity - delta
• X(t) - variable X at time T(delta)
• X(t:t') = {X(t), ..., X(t')} (t<=t'), variables X(t) in t...t'
• Goal: want to represent P(X(t:t')) for any t, t' (predict trajectory between t and t')

Two assumptions of Temporal model

• Assumption 1: Markov assumption
  Given $ (X_{t+1} \perp X_{0:t-1}) | X_t $, is the pre-condition true?

1. if given more variables in same case: for instance, velocity speed, etc.
2. by adding dependent vale in time, calling it semi-Markov

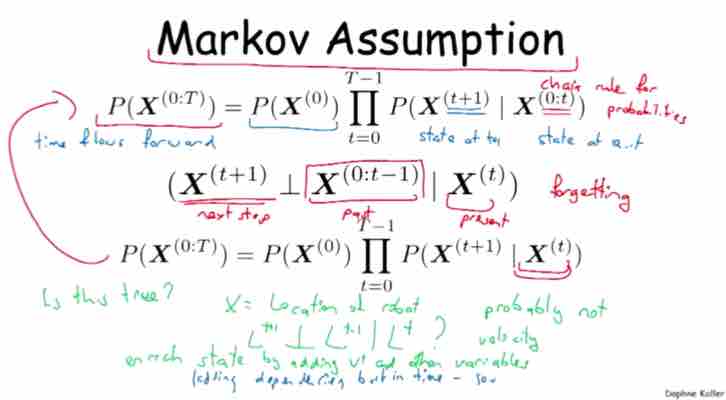
Figure 2-1, Markov Assumption 1